我发现补基础学高数有点来不太急了，而且有时候应用不太上就想先做题来判断自己缺失哪部分知识点然后架构式补充，争取学会这一道题补基础的同时学习做题逻辑！

这道题很简单 就是求导 $$ y = \arcsin(\sin x) $$

高数书上的一道题，是一个很简单的习题

我们先来理解一下这个函数 很明显能看出来这个是一个复合函数 先求出sinx再由sinx的值带入到arcsin里面 首先不理解的点是arcsin的含义 需要先学习一下

先解决arcsin是什么

• $$ \text{arcsin 是反正弦函数，读作“ark-sine”。} $$

  • $$ \text{作用：已知正弦值，求对应的角度。} $$
  • $$\text{定义域：输入可以是 } [-1, 1] \text{ 之间的数。}$$
  • $$\text{值域（输出范围）：} \left[-\frac{\pi}{2}, \frac{\pi}{2}\right] \text{（弧度制），或 } [-90^\circ, 90^\circ] \text{（角度制）。}$$

这样理解可能比较困难我们直接来输出一些值看返回是什么值 $$ \text{arcsin 对这些值的返回结果} $$

其实就是将sin函数在特定定义中反转了 sin函数是输入角度得到正弦值 arcsin则是输入正弦值得到角度

$$\begin{array}{|c|c|c|}\hline\text{输入 } x \text{（正弦值）} & \arcsin x \text{（角度制）} & \arcsin x \text{（弧度制）} \\hline0 & 0^\circ & 0 \\hline\frac{1}{2} & 30^\circ & \frac{\pi}{6} \\hline\frac{\sqrt{2}}{2} & 45^\circ & \frac{\pi}{4} \\hline\frac{\sqrt{3}}{2} & 60^\circ & \frac{\pi}{3} \\hline1 & 90^\circ & \frac{\pi}{2} \\hline-\frac{1}{2} & -30^\circ & -\frac{\pi}{6} \\hline-\frac{\sqrt{2}}{2} & -45^\circ & -\frac{\pi}{4} \\hline-\frac{\sqrt{3}}{2} & -60^\circ & -\frac{\pi}{3} \\hline-1 & -90^\circ & -\frac{\pi}{2} \\hline\end{array}$$

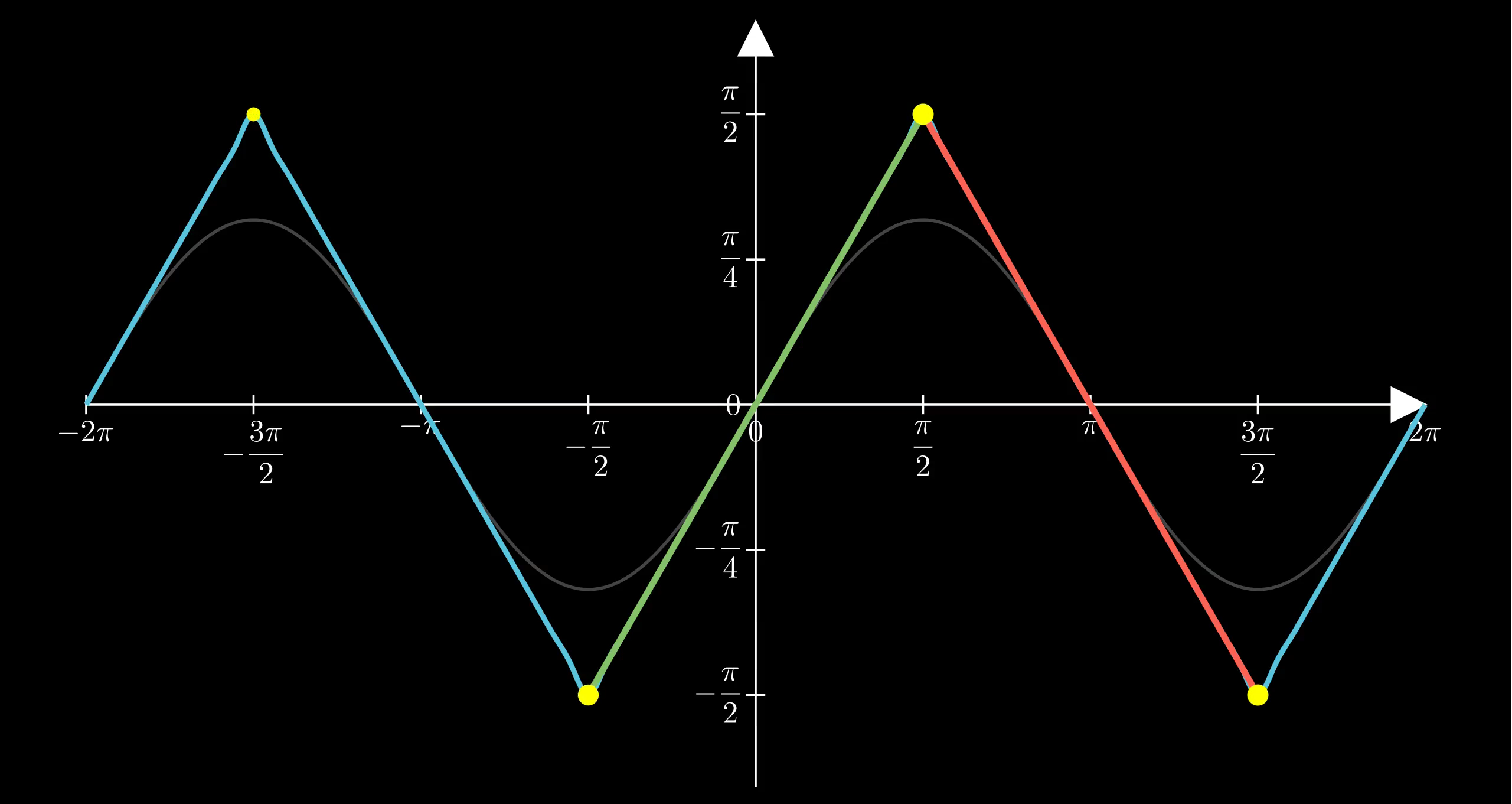
画出 y = arcsin(sin x) 的图像

将一些数代入看一下 让理解的更深刻一点

• 在 [-π/2, π/2] 区间：y = x（一条斜线）
• 在 [π/2, 3π/2] 区间：y = π - x（一条向下斜线）
• 周期为 2π，形状像锯齿波

用Manim画了一个简单的动画如下效果 函数图像就长这个样子

动画Gif（没啥办法了 视频在Markdown支持不是很好 放了一个gif动图）

求导是什么

导数 = 瞬时变化率 = 函数图像的“斜率”

例子：汽车行驶

• 路程 s(t)（米），时间 t（秒）
• 平均速度 = 路程变化 ÷ 时间变化
  比如 2 秒内走了 10 米，平均速度 = 10/2=510/2=5 米/秒

在这道题上比较简单 导数就是曲线在某一点切线的斜率 也就是$y=kx+b$ 中的 $k$

图像法分析这道题的导数（斜率）

我们再看一下这个动画 其实很明显 斜率在1和-1两个值循环 而黄点处正好为转换点

在 x ∈ [-π/2, π/2] 区间：

• 图像是直线 y = x
• 这条直线的斜率是 1
  所以在这个区间内，导数 = 1

在 x ∈ [π/2, 3π/2] 区间：

• 图像是直线 y = π - x
• 斜率是 -1
  所以在这个区间内，导数 = -1

在 x = π/2 点：

• 左边斜率是 1，右边斜率是 -1
• 左右导数不相等 → 导数不存在（图像出现黄点）

那这道题的斜率也就出来啦 如下

$$y’ = \begin{cases}1, & \text{当 } x \in \left(-\dfrac{\pi}{2} + 2k\pi, \dfrac{\pi}{2} + 2k\pi\right) \-1, & \text{当 } x \in \left(\dfrac{\pi}{2} + 2k\pi, \dfrac{3\pi}{2} + 2k\pi\right) \\text{不存在}, & \text{当 } x = \dfrac{\pi}{2} + k\pi\end{cases}\quad (k \in \mathbb{Z})$$

可是这里的图像法需要画图（这里主要是为了理解导数是什么） 如果没有电脑纯靠人力在遇到复杂函数可能画图困难 也就延申出公式推导导数

公式求导法

一开始一看真的头大了

基本三角函数导数

$$ \frac{d}{dx}(\sin x) = \cos x $$

$$ \frac{d}{dx}(\cos x) = -\sin x $$

$$ \frac{d}{dx}(\tan x) = \sec^2 x = 1 + \tan^2 x $$

$$ \frac{d}{dx}(\cot x) = -\csc^2 x = -(1 + \cot^2 x) $$

$$ \frac{d}{dx}(\sec x) = \sec x \tan x $$

$$ \frac{d}{dx}(\csc x) = -\csc x \cot x $$

反三角函数导数（关键公式）

$$ \frac{d}{dx}(\arcsin x) = \frac{1}{\sqrt{1 - x^2}}, \quad |x| < 1 $$

$$ \frac{d}{dx}(\arccos x) = -\frac{1}{\sqrt{1 - x^2}}, \quad |x| < 1 $$

$$ \frac{d}{dx}(\arctan x) = \frac{1}{1 + x^2} $$

$$ \frac{d}{dx}(\mathrm{arccot} , x) = -\frac{1}{1 + x^2} $$

$$ \frac{d}{dx}(\mathrm{arcsec} , x) = \frac{1}{|x|\sqrt{x^2 - 1}}, \quad |x| > 1 $$

$$ \frac{d}{dx}(\mathrm{arccsc} , x) = -\frac{1}{|x|\sqrt{x^2 - 1}}, \quad |x| > 1 $$

复合函数形式（更通用）

$$ \frac{d}{dx}(\arcsin u) = \frac{1}{\sqrt{1 - u^2}} \cdot \frac{du}{dx}, \quad |u| < 1 $$

$$ \frac{d}{dx}(\arccos u) = -\frac{1}{\sqrt{1 - u^2}} \cdot \frac{du}{dx}, \quad |u| < 1 $$

$$ \frac{d}{dx}(\arctan u) = \frac{1}{1 + u^2} \cdot \frac{du}{dx} $$

当我听到这些都要背的时候逐渐有点难绷了（根本一眼看不懂

这里我们不管这么多公式 我们就用能利用到的以下这些

链式法则

核心思想：当函数是”一层套一层”的时候，我们从外到里一层层求导，然后相乘。

通俗比喻

想象你要计算：

• 小明的年龄 = 2 × 小明的学龄
• 小明的学龄 = 他上学的年数

现在问：小明的年龄增长1岁，需要多上几年学？

解答：

1. 年龄对学龄的变化率：每多1年学龄，年龄增加2岁
2. 学龄对上学年数的变化率：每多上1年学，学龄增加1年
3. 所以：年龄对上学年数的变化率 = 2 × 1 = 2

数学表达

如果 $y = f(g(x))$，即：

• 外层：$y = f(u)$，其中 $u = g(x)$
• 内层：$u = g(x)$

那么：$\frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx}$

中文读法：”y对x的导数 = y对u的导数 × u对x的导数”

用公式法求导

设置中间变量

函数如下：$y = \arcsin(\sin x)$ 设置中间变量为$u=sinx$

这有两层：

1. 最外层：$y = \arcsin(u)$ ← 这是”反正弦”函数
2. 中间层：$u = \sin x$ ← 这是”正弦”函数
3. 最内层：$x$ ← 自变量

应用链式法则

链式法则公式带入后如下

$$\frac{dy}{dx} = \frac{d}{du}[\arcsin(u)] \cdot \frac{du}{dx}$$

其中 $u=sin⁡x$

先求外层导数

这里使用这个公式 $$\frac{d}{dx}(\arcsin x) = \frac{1}{\sqrt{1 - x^2}}, \quad \text{其中} \ |x| < 1$$

将$u$带入则为 $$\frac{d}{du}(\arcsin u) = \frac{1}{\sqrt{1 - u^2}}, \quad \text{条件：} \ |u| < 1$$

再求内层导数

这里 $u=sin⁡x$，用到正弦函数的导数公式 $\frac{d}{dx}(sinx)=cosx$

将$u$带入到$$\frac{d}{dx}(sinx)=cosx$$ 可得$$\frac{du}{dx}=cosx$$

用链式法则进行相乘

可得以下导数 $$\frac{dy}{dx}=\frac{1}{\sqrt{1 - u^2}} \cdot cosx$$

使用三角函数基本恒等式

带入$$u=sin⁡x$$ 可得 $$\frac{dy}{dx}=\frac{1}{\sqrt{1 - (sinx)^2}} \cdot cosx$$

使用三角函数基本恒等式：$$\sin^2 x + \cos^2 x = 1$$

所以：$$1 - \sin^2 x = \cos^2 x$$

代入：$\frac{dy}{dx} = \frac{1}{\sqrt{\cos^2 x}} \cdot \cos x$

处理平方根

第六步：处理绝对值

重要概念：$\sqrt{a^2} = |a|$，不是 $a$

因为平方根总是非负数，而 $\cos x$ 可能是正也可能是负。

所以：$\sqrt{\cos^2 x} = |\cos x|$

代入：$\frac{dy}{dx} = \frac{1}{|\cos x|} \cdot \cos x = \frac{\cos x}{|\cos x|}$

分析表达式

这里也就正好说明了 如果$$cosx=0$$函数不可导

$$\frac{\cos x}{|\cos x|} = \begin{cases}1, & \text{当 } \cos x > 0 \-1, & \text{当 } \cos x < 0 \\text{未定义}, & \text{当 } \cos x = 0\end{cases}$$

确定 cos⁡x 的符号区间

这个就是利用$cos$函数图像

1. $\cos x > 0$ 的区间：

$x \in \left(-\frac{\pi}{2} + 2k\pi,\ \frac{\pi}{2} + 2k\pi\right),\quad k \in \mathbb{Z}$

2. $\cos x < 0$ 的区间：

$x \in \left(\frac{\pi}{2} + 2k\pi,\ \frac{3\pi}{2} + 2k\pi\right),\quad k \in \mathbb{Z}$

3. $\cos x = 0$ 的点：

$x = \frac{\pi}{2} + k\pi,\quad k \in \mathbb{Z}$

最终答案

$$y’ = \frac{\cos x}{|\cos x|} = \begin{cases} 1, & \text{当 } x \in \left(-\dfrac{\pi}{2} + 2k\pi,\ \dfrac{\pi}{2} + 2k\pi\right) \-1, & \text{当 } x \in \left(\dfrac{\pi}{2} + 2k\pi,\ \dfrac{3\pi}{2} + 2k\pi\right) \\text{不存在}, & \text{当 } x = \dfrac{\pi}{2} + k\pi\end{cases}\quad (k \in \mathbb{Z})$$

Manim Python代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74

from manim import *
import numpy as np

class ArcsinSinGraph(Scene):
    def construct(self):
        # 创建高质量坐标系 - 关闭默认数字显示
        axes = Axes(
            x_range=[-2*PI, 2*PI, PI/2],
            y_range=[-PI/2 - 0.5, PI/2 + 0.5, PI/4],
            x_length=14,
            y_length=8,
            axis_config={
                "color": WHITE,
                "stroke_width": 2,
                "include_numbers": False,  # 关键：关闭默认数字
                "font_size": 24
            },
        ).scale(0.9)
        
        # 添加π标签到x轴
        x_pi_labels = VGroup()
        x_positions = [-2*PI, -3*PI/2, -PI, -PI/2, 0, PI/2, PI, 3*PI/2, 2*PI]
        x_labels = ["-2\pi", r"-\frac{3\pi}{2}", r"-\pi", r"-\frac{\pi}{2}", "0", 
                   r"\frac{\pi}{2}", r"\pi", r"\frac{3\pi}{2}", "2\pi"]
        
        for x_val, label in zip(x_positions, x_labels):
            tex = MathTex(label, font_size=28, color=WHITE)
            tex.next_to(axes.c2p(x_val, 0), DOWN, buff=0.15)
            x_pi_labels.add(tex)
        
        # 添加π标签到y轴
        y_pi_labels = VGroup()
        y_positions = [-PI/2, -PI/4, 0, PI/4, PI/2]
        y_labels = [r"-\frac{\pi}{2}", r"-\frac{\pi}{4}", "0", r"\frac{\pi}{4}", r"\frac{\pi}{2}"]
        
        for y_val, label in zip(y_positions, y_labels):
            tex = MathTex(label, font_size=28, color=WHITE)
            tex.next_to(axes.c2p(0, y_val), LEFT, buff=0.15)
            y_pi_labels.add(tex)
        
        # 绘制函数
        sin_graph = axes.plot(lambda x: np.sin(x), color=GRAY, stroke_width=3, stroke_opacity=0.5)
        arcsin_graph = axes.plot(
            lambda x: np.arcsin(np.sin(x)), 
            color=BLUE, 
            stroke_width=5
        )
        
        # 高亮关键区间
        line1 = axes.plot(lambda x: x, x_range=[-PI/2, PI/2], color=GREEN, stroke_width=6)
        line2 = axes.plot(lambda x: PI - x, x_range=[PI/2, 3*PI/2], color=RED, stroke_width=6)
        
        # 标记尖角点
        dots = VGroup()
        for point in [PI/2, 3*PI/2, -PI/2, -3*PI/2]:
            dot = Dot(axes.c2p(point, np.arcsin(np.sin(point))), color=YELLOW, radius=0.1)
            dots.add(dot)
        
        # 动画序列
        self.play(Create(axes), run_time=2)
        self.play(
            Write(x_pi_labels),
            Write(y_pi_labels),
            run_time=2
        )
        self.play(Create(sin_graph), run_time=2)
        self.play(Create(arcsin_graph), run_time=3)
        self.play(
            Create(line1),
            Create(line2),
            run_time=2
        )
        self.play(LaggedStart(*[GrowFromCenter(dot) for dot in dots], lag_ratio=0.3))
        self.wait(3)